수학 공식 | 고등학교 > 이산확률변수의 평균과 표준편차
확률질량함수
이산확률변수 $ X $의 각 값 $ x_i $와 $ X $가 $ x_i $를 취할 확률 $ p_i $의 대응 관계를 이산확률변수 $ X $의 확률분포라 하고, 그 관계식
\begin{gather*}
P(X=x_i) = p_i \ (i=1, \ 2, \ 3, \ \cdots, \ n)
\end{gather*}
를 이산확률변수 $ X $의 확률질량함수라 한다.
이산확률변수 $ X $의 확률분포를 표로 나타내면 다음과 같다.

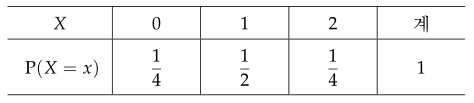
한 개의 동전을 두 번 던지는 시행에서 앞면이 나오는 횟수를 확률변수 $ X $라 할 때, 확률변수 $ X $의 확률분포를 표로 나타내어라.
확률변수 $ X $가 가질 수 있는 값은 $ 0 $, $ 1 $, $ 2 $이다.
확률질량함수의 성질
이산확률변수 $ X $의 확률질량함수
\begin{gather*}
P(X = x_i) = p_i \ (i = 1, \ 2, \ 3, \ \cdots, \ n)
\end{gather*}
는 다음과 같은 성질을 가진다.
- $ \displaystyle 0 \leq p_i \leq 1 $
- $ \displaystyle \sum_{i=1}^{n} p_i = 1 $
- $ \displaystyle P(x_i \leq X \leq x_j) = \sum_{k=i}^{j} p_k \ \ (i, \ j = 1, \ 2, \ \cdots, \ n, \ \ i \leq j ) $
이산확률변수의 평균, 분산, 표준편차
이산확률변수 $ X $의 확률질량함수
\begin{gather*}
P(X = x_i) = p_i \ (i = 1, \ 2, \ 3, \ \cdots, \ n)
\end{gather*}
의 평균 $ {E(X)} $, 분산 $ {V(X)} $, 표준편차 $ \sigma(X) $은 다음과 같다.
- $ \displaystyle {E(X)} = \sum_{i=1}^{n} x_i p_i $
- $ \displaystyle {V(X)} = \sum_{i=1}^{n} (x_i - m)^2 p_i $
- $ \sigma(X) = \sqrt{V(X)} $
- $ {E(X)} = m $, $ {V(X)} = \sigma^2 $, $ \sigma(X) = \sigma $로 나타내기도 한다.
- 분산은 다음과 같이 구할 수도 있다.
\begin{align*}
V(X) &= \sum_{i=1}^{n} ({x_i}^2 - 2mx_i + m^2) p_i \\
&= \sum_{i=1}^{n} {x_i}^2 p_i - 2m \sum_{i=1}^{n} x_i pi + m^2 \sum_{i=1}^{n} p_i \\
&= \sum_{i=1}^{n} {x_i}^2 p_i - 2m^2 + m^2 \\
&= E(X^2) - E(X)^2
\end{align*}
확률변수 $ X $의 확률분포가 다음 표와 같을 때, 평균과 분산을 구하여라.
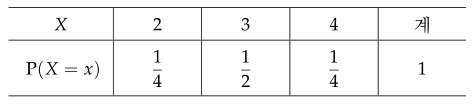
$ \displaystyle E(X) = 2 \times \frac{1}{4} + 3 \times \frac{1}{2} + 4 \times \frac{1}{4} = 3 $
$ \displaystyle V(X) = 2^2 \times \frac{1}{4} + 3^2 \times \frac{1}{2} + 4^2 \times \frac{1}{4} - 3^2 = \frac{1}{2} $
평균, 분산, 표준편차의 성질
확률변수 $ X $와 상수 $ a $, $ b $에 대하여 다음이 성립한다.
- $ {E}(a{X}+b) = a {E(X)} + b $
- $ {V}(a{X}+b) = a^2 {V(X)} $
- $ \sigma(a{X}+b) = |a| \sigma({X}) $
확률변수 $ X $에 대하여 $ E(X) = 10 $, $ V(X) = 9 $이다.
\begin{gather*}
Y = 3X + 9
\end{gather*}
일 때, $ E(Y) $와 $ V(Y) $를 구하여라.
$ E(Y) = E(3X+9) = 3 E(X) + 9 = 3 \times 10 + 9 = 39 $
$ V(Y) = V(3X+9) = 3^2 V(X) = 3^2 \times 9 = 81 $