MATH FACTORY

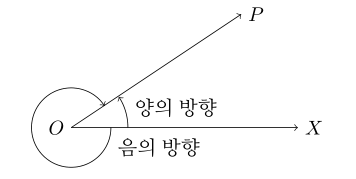
1. $ \angle XOP $의 크기는 반직선 $ OX $의 위치에서 반직선 $ OP $가 점 $ O $를 중심으로 회전한 양이다.
2. 이때 반직선 $ OX $를 시초선, 반직선 $ OP $를 동경이라고 한다.
3. 동경 $ OP $가 점 $ O $를 중심으로 회전할 때, 시계 바늘이 도는 방향과 반대 방향을 양의 방향, 시계 바늘이 도는 방향과 같은 방향을 음의 방향이라 한다.
4. 각의 크기는 회전 방향이 양의 방향이면 양의 부호($ + $), 음의 방향이면 음의 부호($ - $)를 붙여 나타낸다.

$ \angle XOP $의 크기의 하나를 $ \alpha^\circ $라고 할 때, 동경 $ OP $로 정해지는 각의 크기는 다음과 같이 나타낼 수 있다.

\begin{gather*}
360^\circ \times n + \alpha^\circ \ \ (\textrm{단, }n\textrm{은 정수})
\end{gather*}

이것을 동경 $ OP $가 나타내는 일반각이라고 한다.

좌표평면에서 각의 꼭짓점을 원점 $ O $로 잡고, 시초선 $ OX $를 $ x $축의 양의 방향으로 잡을 때, 동경 $ OP $가 제$ 1 $사분면, 제$ 2 $사분면, 제$ 3 $사분면, 제$ 4 $사분면에 있으면 동경 $ OP $가 나타내는 각을 각각 제$ 1 $사분면의 각, 제$ 2 $사분면의 각, 제$ 3 $사분면의 각, 제$ 4 $사분면의 각이라고 한다. 동경 $ OP $가 좌표축 위에 놓여 있을 때는 어느 사분면에도 속하지 않는다.

$ n $이 정수일 때

1. 각 $ \theta $가 제$ 1 $사분면의 각이면
   $ 360^\circ \times n < \theta < 360^\circ \times n + 90^\circ $
2. 각 $ \theta $가 제$ 2 $사분면의 각이면
   $ 360^\circ \times n + 90^\circ < \theta < 360^\circ \times n + 180^\circ $
3. 각 $ \theta $가 제$ 3 $사분면의 각이면
   $ 360^\circ \times n + 180^\circ < \theta < 360^\circ \times n + 270^\circ $
4. 각 $ \theta $가 제$ 4 $사분면의 각이면
   $ 360^\circ \times n + 270^\circ < \theta < 360^\circ \times n + 360^\circ $
   \end{jbKeyPointPnume}

두 각 $ \alpha $, $ \beta $를 나타내는 동경에 대하여 다음이 성립한다. (단, $ n $은 정수)

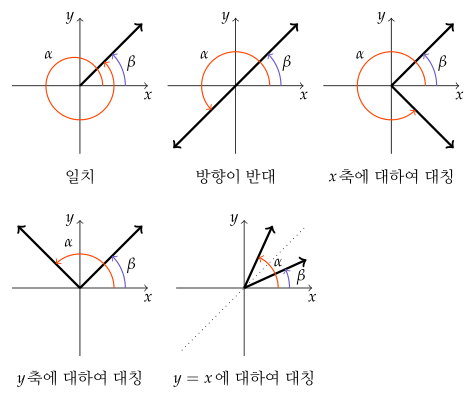
1. 일치 : $ \alpha - \beta = 360^\circ \times n $
2. 일직선 위에 있고 방향이 반대 : \\ $ \alpha - \beta = 360^\circ \times n + 180^\circ $
3. $ x $축에 대하여 대칭 : $ \alpha + \beta = 360^\circ \times n $
4. $ y $축에 대하여 대칭 : $ \alpha + \beta = 360^\circ \times n + 180^\circ $
5. $ y=x $에 대하여 대칭 : $ \alpha + \beta = 360^\circ \times n + 90^\circ $

1. 반지름의 길이와 호의 길이가 같을 때의 중심각의 크기를 $ 1 $라디안(radian)이라 하고 이것을 단위로 각을 나타내는 방법을 호도법이라 한다.
2. $ 1 \mathrm{rad} = \dfrac{180^\circ}{\pi}, \ 1^\circ = \dfrac{\pi}{180} \mathrm{rad} $

반지름의 길이가 $ r $, 중심각의 크기가 $ \theta $(라디안)인 부채꼴에서

1. 호의 길이 : $ l = r \theta $
2. 넓이 : $ S = \dfrac{1}{2} r^2 \theta = \dfrac{1}{2} rl $