수학 공식 | 고등학교 > 로그함수의 뜻과 그래프
로그함수의 뜻
$ a $가 $ 1 $이 아닌 양수일 때 양의 실수 $ x $를 $ \log_a x $에 대응시키는 함수
\begin{gather*}
y = \log_a x
\end{gather*}
를 $ a $를 밑으로 하는 로그함수라고 한다.
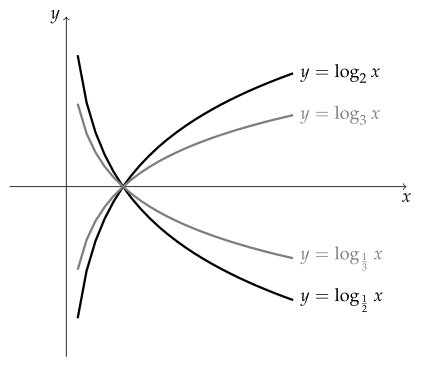
로그함수 $ \boldsymbol{y=\log_a x \ ( a > 0, \ a \neq 1)} $의 성질
- 정의역은 양의 실수 전체의 집합이다.
- 치역은 실수 전체의 집합이다.
- 항상 $ (1, \ 0) $을 지난다.
- $ a > 1 $이면 $ x $의 값이 커질 때 $ y $의 값이 커지고, $ 0 < a < 1 $이면 $ x $의 값이 증가할 때 $ y $의 값이 감소한다.
- 점근선은 $ y $축($ x=0 $)이다.
- $ a > 1 $이면 $ a $의 값이 커질수록, $ 0 < a < 1 $이면 $ a $의 값이 작아질수록 그래프는 $ x $축에 가까워진다.
로그함수의 평행이동과 대칭이동
로그함수 $ y=\log_a x $의 그래프를
- $ x $축의 방향으로 $ m $만큼, $ y $축의 방향으로 $ n $만큼 평행이동 ⇨ $ y=\log_a (x-m)+n $
- $ x $축에 대하여 대칭이동 ⇨ $ y=-\log_a x $
- $ y $축에 대하여 대칭이동 ⇨ $ y=\log_a (-x) $
- 원점에 대하여 대칭이동 ⇨ $ y=-\log_a (-x) $
지수함수와 로그함수와의 관계
지수함수 $ y = a^x $와 로그함수 $ y=\log_a x $는 역함수 관계이고, 그래프는 $ y=x $에 대하여 대칭이다.
로그함수의 최대와 최소
- $ y = \log_a x $의 꼴인 경우 정의역의 양 끝에서 최대 또는 최소가 된다.
- $ y = \log_a {f(x)} $의 꼴인 경우 $ f(x) = t $로 치환하여 푼다.
- $ y = f(\log_a x) $의 꼴인 경우 $ \log_a x = t $로 치환하여 푼다.
- 지수에 로그가 있는 경우 양변에 로그를 취하여 푼다.
$ 1 \leq x \leq 16 $일 때, 다음 함수의 최댓값과 최솟값을 구하여라.
\begin{gather*}
y = \log_2 x
\end{gather*}
$ \log_2 1 \leq \log_2 x \leq \log_2 16 $이므로 최댓값은 $ 4 $, 최솟값은 $ 0 $이다.
$ 1 \leq x \leq 4 $일 때, 다음 함수의 최댓값과 최솟값을 구하여라.
\begin{gather*}
y = \log_2 (x^2 - 4x + 8)
\end{gather*}
$ t = x^2 - 4x + 8 = (t-2)^2 + 4 $
$ 1 \leq x \leq 4 $이면 $ 4 \leq t \leq 8 $이고 $ \log_2 4 \leq \log_2 t \leq \log_2 8 $
따라서 최댓값은 $ 3 $, 최솟값은 $ 2 $이다.
$ 2 \leq x \leq 16 $일 때, 함수 $ y = ( \log_2 x )^2 - \log_2 x^4 + 2 $의 최댓값과 최솟값을 구하여라.
$ t = \log_2 x $로 놓으면 $ 1 \leq t \leq 4 $
$ y = t^2 - 4t + 2 = (t-2)^2 - 2 $이므로 최댓값은 $ 2 $, 최솟값은 $ -2 $이다.
함수 $ y=100x^{\log x} $의 최솟값을 구하여라.
양변에 상용로그를 취하면 $ \log y = 2 + (\log x)^2 \geq 2 $
$ \log y $의 최솟값이 $ 2 $이므로 $ y $의 최솟값은 $ 100 $이다.