수학 공식 | 고등학교 > 이차부등식
이차함수의 그래프와 이차부등식의 해
이차방정식 $ ax^2+bx+c=0 \ (a>0) $의 판별식 $ D $의 부호에 따른 이차함수 $ y=ax^2+bx+c $의 그래프와 이차부등식의 해는 다음과 같다.
$ D > 0 $일 때
$ y = ax^2 + bx + c $의 그래프
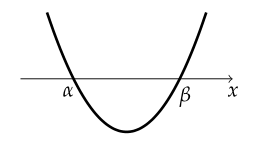
- $ ax^2 + bx + c > 0 $의 해 : $ x < \alpha $ 또는 $ x > \beta $
- $ ax^2 + bx + c \geq 0 $의 해 : $ x \leq \alpha $ 또는 $ x \geq \beta $
- $ ax^2 + bx + c < 0 $의 해 : $ \alpha < x < \beta $
- $ ax^2 + bx + c \leq 0 $의 해 : $ \alpha \leq x \leq \beta $
$ D = 0 $일 때
$ y = ax^2 + bx + c $의 그래프
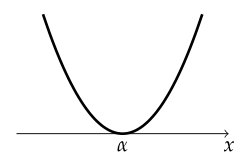
- $ ax^2 + bx + c > 0 $의 해 : $ x \neq \alpha $인 모든 실수
- $ ax^2 + bx + c \geq 0 $의 해 : 모든 실수
- $ ax^2 + bx + c < 0 $의 해 : 없다
- $ ax^2 + bx + c \leq 0 $의 해 : $ x = \alpha $
$ D < 0 $일 때
$ y = ax^2 + bx + c $의 그래프
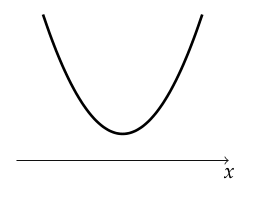
- $ ax^2 + bx + c > 0 $의 해 : 모든 실수
- $ ax^2 + bx + c \geq 0 $의 해 : 모든 실수
- $ ax^2 + bx + c < 0 $의 해 : 없다
- $ ax^2 + bx + c \leq 0 $의 해 : 없다
이차부등식이 항상 성립할 조건]
이차방정식 $ ax^2 + bx + c = 0 $의 판별식을 $ D $라 할 때
- 모든 실수 $ x $에 대하여 $ ax^2 + bx + c > 0 $이 성립할 조건
\begin{gather*}
a > 0, \ \ D < 0
\end{gather*} - 모든 실수 $ x $에 대하여 $ ax^2 + bx + c \geq 0 $이 성립할 조건
\begin{gather*}
a > 0, \ \ D \leq 0
\end{gather*} - 모든 실수 $ x $에 대하여 $ ax^2 + bx + c < 0 $이 성립할 조건
\begin{gather*}
a < 0, \ \ D < 0
\end{gather*} - 모든 실수 $ x $에 대하여 $ ax^2 + bx + c \leq 0 $이 성립할 조건
\begin{gather*}
a < 0, \ \ D \leq 0
\end{gather*}
연립이차부등식
연립부등식을 이루는 각각의 부등식의 해를 구한 후 이들의 공통부분을 구한다.
2018/06/20 09:28수학 공식