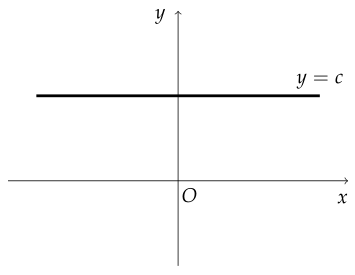수학 공식 | 고등학교 > 함수와 그래프
대응
- 두 집합 $ {X} $, $ {Y} $에 대하여 집합 $ {X} $의 원소에 집합 $ {Y} $의 원소를 짝지은 것을 집합 $ {X} $에서 집합 $ {Y} $로의 대응이라고 한다.
- 이때 집합 $ {X} $의 원소 $ x $에 집합 $ {Y} $의 원소 $ y $가 짝 지어지면 $ x $에 $ y $가 대응한다고 하며, 기호로
\begin{gather*}
x \longrightarrow y
\end{gather*}와 같이 나타낸다.
함수
두 집합 $ {X} $, $ {Y} $에 대하여 집합 $ {X} $의 각 원소에 집합 $ {Y} $의 원소가 오직 하나씩 대응할 때, 이 대응을 집합 $ {X} $에서 집합 $ {Y} $로의 함수라 한다. 이 함수를 $ f $라 하면 기호로
\begin{gather*}
f : {X} \longrightarrow {Y}
\end{gather*}
와 같이 나타낸다.
- 함수를 나타낼 때에는 보통 $ f $, $ g $, $ h $와 같은 알파벳 소문자를 사용한다.
정의역, 공역, 치역
- 함수 $ f : {X} \longrightarrow {Y} $에서 집합 $ {X} $를 함수 $ f $의 정의역, 집합 $ {Y} $를 함수 $ f $의 공역이라 한다.
- 함수 $ f : {X} \longrightarrow {Y} $에서 정의역 $ {X} $의 원소 $ x $에 공역 $ {Y} $의 원소 $ y $가 대응할 때, 기호로
\begin{gather*}
y=f(x)
\end{gather*}와 같이 나타내고, $ f(x) $를 $ x $에서의 함숫값이라 한다. 이때 함숫값 전체의 집합
\begin{gather*}
\{ f(x) \ | \ x \in {X} \}
\end{gather*}를 함수 $ f $의 치역이라 한다.
- 함수 $ y=f(x) $의 정의역이나 공역이 주어져 있지 않은 경우, 정의역은 $ f(x) $가 정의되는 실수 $ x $의 값 전체의 집합으로, 공역은 실수 전체의 집합으로 생각한다.
정의역이 $ \{ -2, \ 0, \ 2 \} $인 함수 $ f(x) = x^3 $의 치역을 구하여라.
$ f(-2) = -8 $, $ f(0) = 0 $, $ f(2) = 8 $이므로 치역은 $ \{ -8, \ 0, \ 8 \} $이다.
서로 같은 함수
두 함수 $ f $, $ g $에 대하여
- 정의역과 공역이 각각 같고
- 정의역의 각 원소 $ x $에 대하여 $ f(x)=g(x) $
일 때, 두 함수 $ f $와 $ g $는 서로 같다고 하고, 기호로
\begin{gather*}
f=g
\end{gather*}
와 같이 나타낸다.
- 두 함수 $ f $와 $ g $가 서로 같지 않을 때는 기호로 $ f \neq g $와 같이 나타낸다.
정의역이 $ \{ -1, \ 0, \ 1 \} $인 두 함수 $ f(x)=x^2 $, $ g(x)=x^4 $는 같은가?
$ f(-1) = g(-1) = 1 $, $ f(0) = g(0) = 0 $, $ f(1) = g(1) = 1 $이므로 두 함수는 같다.
함수의 그래프
- 함수 $ f : X \longrightarrow Y $에서 정의역 $ X $의 원소 $ x $와 이에 대응하는 함숫값 $ f(x) $의 순서쌍 전체의 집합
\begin{gather*}
G= \{ (x, \ f(x)) | x \in X \}
\end{gather*}를 함수 $ f $의 그래프라고한다. - 순서쌍 $ (x, \ f(x)) $는 좌표평면 위의 점 $ (x, \ f(x)) $에 대응하므로 그래프 $ G $를 점의 집합으로 생각하여 좌표평면 위에 나타낼 수 있다.
- 좌표평면 위의 함수의 그래프는 정의역의 각 원소 $ a $에 대하여 직선 $ x=a $와 오직 한 점에서 만난다.
왼쪽은 함수의 그래프이고, 오른쪽은 함수의 그래프가 아니다.
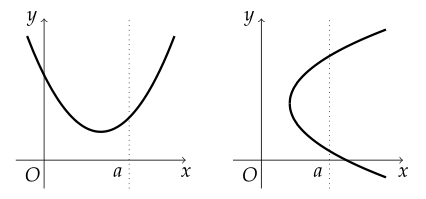
일대일함수
함수 $ f : {X} \rightarrow {Y} $에서 정의역 $ {X} $의 임의의 두 원소 $ x_1 $, $ x_2 $에 대하여
$ x_1 \neq x_2 $이면 $ f( x_1 ) \neq f( x_2 ) $
가 성립할 때, 함수 $ f $를 일대일함수라 한다.
예를 들어 $ f(x) = 2x $는 일대일함수이다. $ x_1 \neq x_2 $일 때
\begin{gather*}
f(x_1) - f(x_2) = 2x_1 - 2x_2 = 2(x_1 - x_2) \neq 0 \\
\therefore \ \ f(x_1) \neq f(x_2)
\end{gather*}
이기 때문이다.
반면 $ f(x) = x^2 $은 일대일함수가 아니다. $ f(-1) = f(1) = 1 $로, 서로 다른 정의역의 원소 $ -1 $과 $ 1 $에 대하여 함숫값이 같기 때문이다.
일대일대응
함수 $ f : {X} \rightarrow {Y} $가 일대일함수이면서 치역과 공역이 같을 때, 이 함수를 일대일대응이라 한다.
정의역과 치역이 실수의 집합일 때 일대일대응을 그래프로 나타내면, $ x $축과 평행한 직선을 그었을 때, $ y $축과 평행한 직선을 그었을 때 교점이 하나만 있다.
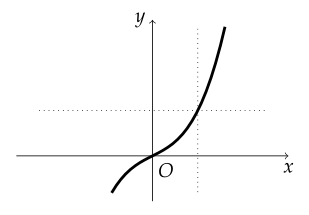
따라서 일대일대응의 그래프는 계속 증가하거나 계속 감소한다.
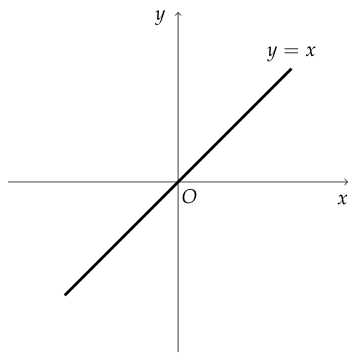
항등함수
함수 $ f : {X} \rightarrow {Y} $에서 정의역 $ {X} $의 임의의 원소 $ x $에 대하여
\begin{gather*}
f(x)=x
\end{gather*}
이 성립할 때, 함수 $ f $를 집합 $ {X} $에서의 항등함수라고 한다.
정의역이 실수 전체의 집합일 때, 항등함수를 그래프로 나타내면 다음과 같다.
상수함수
함수 $ f : {X} \rightarrow {Y} $에서 정의역 $ {X} $의 모든 원소 $ x $에 대하여
\begin{gather*}
f(x)=c \ (c\textrm{는 상수})
\end{gather*}
일 때, 이 함수를 상수함수라 한다.
정의역이 실수 전체의 집합일 때, 상수함수를 그래프로 나타내면 다음과 같다.