수학 공식 | 고등학교 > 평행이동
평행이동
도형을 모양과 크기를 바꾸지 않고 일정한 방향으로 일정한 거리만큼 옮기는 것을 평행이동이라고 한다.
점의 평행이동
좌표평면 위의 한 점 $ P(x, \ y) $를 $ x $축의 방향으로 $ a $만큼, $ y $축의 방향으로 $ b $만큼 평행이동한 점 $ P' $의 좌표는
\begin{gather*}
P'(x+a, \ y+b)
\end{gather*}
도형의 평행이동
방정식 $ f(x, \ y)=0 $이 나타내는 도형을 $ x $축의 방향으로 $ a $만큼, $ y $축의 방향으로 $ b $만큼 평행이동한 도형의 방정식은
\begin{gather*}
f(x-a, \ y-b) = 0
\end{gather*}
좌표평면에서 방정식 $ f(x, \ y)=0 $이 나타내는 도형을 $ F $, 도형 $ F $를 $ x $축의 방향으로 $ a $만큼, $ y $축의 방향으로 $ b $만큼 평행이동한 도형을 $ F' $이라 하자.
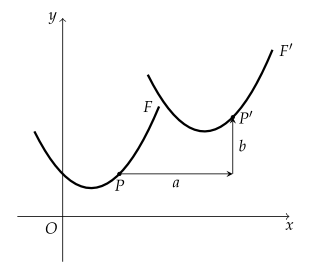
도형 $ F $ 위의 점을 $ P(m, \ n) $이라 하면
\begin{gather*}
f(m, \ n)=0
\end{gather*}
점 $ P $를 $ x $축의 방향으로 $ a $만큼, $ y $축의 방향으로 $ b $만큼 평행이동한 점을 $ P'(x, \ y) $라 하면
\begin{gather*}
x = m+a, \ \ y = n+b \ \ \ \therefore \ \ m = x-a, \ \ n = y-b
\end{gather*}
$ f(m, \ n)=0 $에 대입하면
\begin{gather*}
f(x-a, \ y-b) = 0
\end{gather*}
직선 $ y=2x+1 $을 $ x $축의 방향으로 $ 2 $만큼, $ y $축의 방향으로 $ 1 $만큼 평행이동한 도형의 방정식을 구하여라.
$ x $ 대신에 $ x-2 $, $ y $ 대신에 $ y-1 $을 대입한다.
\begin{gather*}
y-1 = 2(x-2) + 1 \ \ \therefore \ \ y=2x-2
\end{gather*}