원의 극선의 방정식
원의 극선
원 밖의 한 점에서 원에 그은 두 접선이 있을 때, 두 접점을 지나는 직선을 원의 극선이라 합니다.
극선의 방정식을 구하는 것은 고등학교 교과서에 있는 내용은 아니지만, 학교에서 어려운 문제를 출제하고 싶을 때 나올 수 있습니다.
공식 자체는 간단하니 외워두도록 합니다.
원의 극선의 방정식
원 $ x^2 + y^2 = r^2 $이 있을 때, 원 밖의 점 $ ( x_1, \ y_1 ) $에서 원에 접선을 두 개 그을 수 있습니다. 이때 두 접점의 좌표를 각각 $ ( a, \ b ) $, $ ( c, \ d ) $라 하면, 두 점을 지나는 직선이 극선입니다.
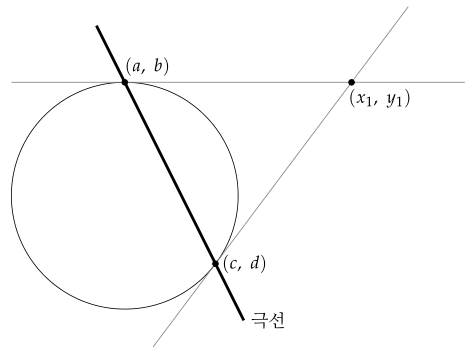
원 위의 점 $ ( a, \ b ) $에서의 접선의 방정식은 $ ax + by = r^2 $이고, 이 접선이 $ ( x_1, \ y_1 ) $을 지나므로
\begin{gather*}
ax_1 + by_1 = r^2
\end{gather*}
입니다. 마찬가지 방식으로, 점 $ ( c, \ d ) $에서의 접선의 방정식은 $ cx + dy = r^2 $이고, 이 접선이 $ ( x_1, \ y_1 ) $을 지나므로
\begin{gather*}
cx_1 + dy_1 = r^2
\end{gather*}
입니다.
직선 $ x_1 x + y_1 y = r^2 $에 점 $ ( a, \ b ) $를 대입하면
\begin{gather*}
ax_1 + by_1 = r^2
\end{gather*}
이고, 점 $ ( c, \ d ) $를 대입하면
\begin{gather*}
cx_1 + dy_1 = r^2
\end{gather*}
이므로, 점 $ ( a, \ b ) $와 점 $ ( c, \ d ) $를 지나는 직선의 방정식, 즉 극선의 방정식은
\begin{gather*}
x_1 x + y_1 y = r^2
\end{gather*}
입니다.