수학 공식 | 고등학교 > 포물선의 뜻과 포물선의 방정식
포물선의 정의
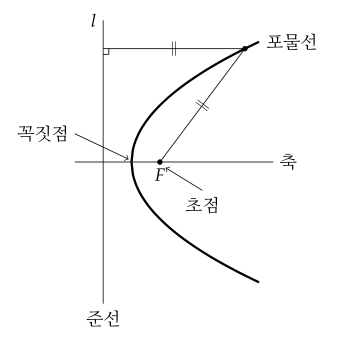
- 평면 위의 한 정점 $ F $와 그 점을 지나지 한 정직선 $ l $과의 거리가 같은 점들의 집합을 포물선이라고 한다.
- 이때 점 $ F $를 초점, 직선 $ l $을 준선, 초점 $ F $를 지나고 준선 $ l $에 수직인 직선을 축, 축과 포물선이 만나는 점을 꼭짓점이라고 한다.
포물선의 방정식
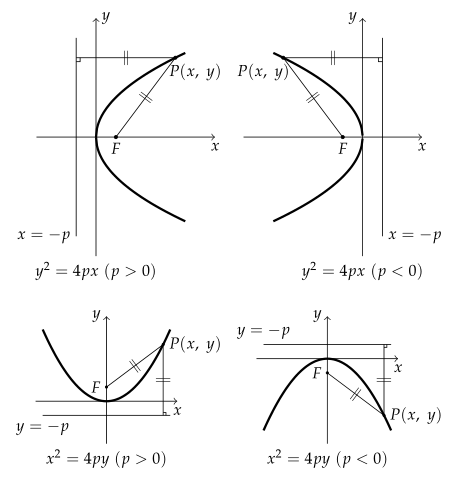
- 초점이 $ F(p, \ 0) $, 준선이 $ x=-p $인 포물선의 방정식
\begin{gather*}
y^2 = 4px \ \ (\textrm{단}, \ \ p \neq 0)
\end{gather*} - 초점이 $ F(0, \ p) $, 준선이 $ y=-p $인 포물선의 방정식
\begin{gather*}
x^2 = 4py \ \ (\textrm{단}, \ \ p \neq 0)
\end{gather*}
- 초점을 $ F(p, \ 0) $, 준선을 $ x=-p $로 하는 포물선 위의 임의의 점을 $ P(x, \ y) $라 하면, 점 $ P $와 점 $ F $ 사이의 거리는
\begin{gather*}
\sqrt{(x-p)^2+y^2}
\end{gather*}이고, 점 $ P $와 직선 $ x=-p $ 사이의 거리는
\begin{gather*}
\left| x-(-p) \right|
\end{gather*}포물선의 정의에 의하여 두 값은 같아야 하므로
\begin{gather*}
\sqrt{(x-p)^2+y^2} = \left| x-(-p) \right|
\end{gather*}양변을 제곱하여 정리하면
\begin{gather*}
y^2 = 4px
\end{gather*} - 초점을 $ F(0, \ p) $, 준선을 $ y=-p $로 하는 포물선 위의 임의의 점을 $ P(x, \ y) $라 하면, 점 $ P $와 점 $ F $ 사이의 거리는
\begin{gather*}
\sqrt{x^2+(y-p)^2}
\end{gather*}이고, 점 $ P $와 직선 $ y=-p $ 사이의 거리는
\begin{gather*}
\left| y-(-p) \right|
\end{gather*}포물선의 정의에 의하여 두 값은 같아야 하므로
\begin{gather*}
\sqrt{x^2+(y-p)^2} = \left| y-(-p) \right|
\end{gather*}양변을 제곱하여 정리하면
\begin{gather*}
x^2 = 4py
\end{gather*}
초점이 $ F(2, \ 0) $, 준선이 $ x=-2 $인 포물선의 방정식을 구하여라.
$ y^2 = 4px $에서 $ p=2 $이므로 $ y^2 = 8x $
초점이 $ F(0, \ -3) $, 준선이 $ y=3 $인 포물선의 방정식을 구하여라.
$ x^2 = 4py $에서 $ p=-3 $이므로 $ x^2 = -12y $
포물선의 평행이동
- 포물선 $ y^2=4px $를 $ x $축 방향으로 $ m $만큼, $ y $축 방향으로 $ n $만큼 평행이동시킨 포물선의 방정식은
\begin{gather*}
(y-n)^2 = 4p(x-m)
\end{gather*}초점의 좌표 : $ (p+m, \ n) $
준선의 방정식 : $ x=-p+m $
축의 방정식 : $ y=n $
꼭짓점의 좌표 : $ (m, \ n) $ - 포물선 $ x^2=4py $를 $ x $축 방향으로 $ m $만큼, $ y $축 방향으로 $ n $만큼 평행이동시킨 포물선의 방정식은
\begin{align*}
(x-m)^2 = 4p(y-n)
\end{align*}초점의 좌표 : $ (m, \ p+n) $
준선의 방정식 : $ y=-p+n $
축의 방정식 : $ x=m $
꼭짓점의 좌표 : $ (m, \ n) $
포물선 $ (y-3)^2 = 12(x+1) $의 초점의 좌표, 준선의 방정식, 꼭짓점의 좌표를 구하여라.
$ (y-3)^2 = 12(x+1) $는 $ y^2 = 12x $를 $ x $축의 방향으로 $ -1 $만큼, $ y $축의 방향으로 $ 3 $만큼 평행이동한 것이다.
$ y^2 = 12x $의 초점의 좌표는 $ (3, \ 0) $, 준선의 방정식은 $ x=-3 $, 꼭짓점의 좌표는 $ (0, \ 0) $이므로, $ (y-3)^2 = 12(x+1) $의 초점의 좌표는 $ (2, \ 3) $, 준선의 방정식은 $ x=-4 $, 꼭짓점의 좌표는 $ (-1, \ 3) $이다.
포물선 $ (x-2)^2 = -8(y-3) $의 초점의 좌표, 준선의 방정식, 꼭짓점의 좌표를 구하여라.
$ (x-2)^2 = -8(y-3) $은 $ x^2 = -8y $를 $ x $축의 방향으로 $ 2 $만큼, $ y $축의 방향으로 $ 3 $만큼 평행이동한 것이다.
$ x^2 = -8y $의 초점의 좌표는 $ (0, \ -2) $, 준선의 방정식은 $ y=2 $, 꼭짓점의 좌표는 $ (0, \ 0) $이므로, $ (x-2)^2 = -8(y-3) $의 초점의 좌표는 $ (2, \ 1) $, 준선의 방정식은 $ y=5 $, 꼭짓점의 좌표는 $ (2, \ 3) $이다.
포물선의 방정식의 일반형
- $ x $축에 평행한 축을 가진 포물선의 방정식
\begin{gather*}
y^2 + Ax + By + C = 0 \ \ (\textrm{단}, \ A \neq 0)
\end{gather*} - $ y $축에 평행한 축을 가진 포물선의 방정식
\begin{gather*}
x^2+Ax+By+C=0 \ \ (\textrm{단}, \ B \neq 0)
\end{gather*}
- $ x $축에 평행한 축을 가진 포물선의 방정식은
\begin{gather*}
(y-n)^2 = 4p(x-m)
\end{gather*}이고, 이 식을 전개하고 정리하면
\begin{gather*}
y^2 - 4px -2ny + n^2 + 4pm = 0
\end{gather*}이다. 즉,
\begin{gather*}
y^2 + Ax + By + C = 0 \ \ (\textrm{단}, \ A \neq 0)
\end{gather*}꼴의 이차식이라면 $ x $축에 평행한 축을 가진 포물선의 방정식이다. - $ y $축에 평행한 축을 가진 포물선의 방정식은
\begin{gather*}
(x-m)^2 = 4p(y-n)
\end{gather*}이고, 이 식을 전개하고 정리하면
\begin{gather*}
x^2 - 2mx - 4py + m^2 + 4pn = 0
\end{gather*}이다. 즉,
\begin{gather*}
x^2+Ax+By+C=0 \ \ (\textrm{단}, \ B \neq 0)
\end{gather*}꼴의 이차식이라면 $ y $축에 평행한 축을 가진 포물선의 방정식이다.
포물선 $ y^2 + 4x - 4y = 0 $의 초점의 좌표를 구하여라.
$ y^2 - 4y + 4 = -4x + 4 \ \ \ \therefore \ \ (y-2)^2 = - 4(x-1) $
$ (y-2)^2 = - 4(x-1) $은 $ y^2 = -4x $를 $ x $축의 방향으로 $ 1 $만큼, $ y $축의 방향으로 $ 2 $만큼 평행이동한 것이다. $ y^2 = -4x $의 초점의 좌표는 $ (-1, \ 0) $이므로 $ (y-2)^2 = - 4(x-1) $의 초점의 좌표는 $ (0, \ 2) $이다.
포물선 $ x^2 + 4x - 4y - 8 = 0 $의 초점의 좌표를 구하여라.
$ x^2 + 4x + 4 = 4y - 4 \ \ \ \therefore \ \ (x+2)^2 = 4(y-1) $
$ (x+2)^2 = 4(y-1) $은 $ x^2 = 4y $를 $ x $축의 방향으로 $ -2 $만큼, $ y $축의 방향으로 $ 1 $만큼 평행이동한 것이다. $ x^2 = 4y $의 초점의 좌표는 $ (0, \ 1) $이므로 $ (x+2)^2 = 4(y-1) $의 초점의 좌표는 $ (-2, \ 2) $이다.