수학 공식 | 중학교 > 소인수분해
소수와 합성수
- $ 1 $보다 큰 자연수 중에서 약수가 $ 1 $과 자기 자신뿐인 수를 소수라 한다.
- $ 1 $보다 큰 자연수 중에서 소수가 아닌 수를 합성수라 한다.
- 소수의 약수는 $ 2 $개이고, 합성수의 약수는 $ 3 $개 이상이다.
- $ 2^2 $, $ 3^2 $ 등 소수의 제곱의 약수는 $ 3 $개이다.
- $ 1 $은 소수도 아니고 합성수도 아니다.
- $ 2 $는 유일한 짝수인 소수이다.
거듭제곱
- 같은 수나 문자를 여러 번 곱한 것을 간단히 나타낸 것을 거듭제곱이라 한다.
- $ a $를 $ n $번 곱한 것을 $ a $의 $ n $제곱이라 하고, 기호로
\begin{gather*}
a^n
\end{gather*}과 같이 나타낸다. 이때 $ a $를 밑, $ n $을 지수라 한다. - $ a $, $ a^2 $, $ a^3 $, $ \cdots $을 통틀어 $ a $의 거듭제곱이라 한다.
인수와 소인수
- 자연수 $ a $, $ b $, $ c $에 대하여
\begin{gather*}
a = b \times c
\end{gather*}일 때, $ b $, $ c $를 $ a $의 인수라고 한다. - 인수 중에서 소수인 것을 소인수라 한다.
소인수분해
$ 1 $보다 큰 자연수를 소인수만의 곱으로 나타내는 것을 소인수분해한다고 한다.
약수와 약수의 개수
자연수 $ N $이
\begin{gather*}
N = a^m \times b^n \ \ (a, \ b\textrm{는 서로 다른 소수}, m, \ n\textrm{은 자연수})
\end{gather*}
로 소인수분해될 때
- $ N $의 약수 : ($ a^m $의 약수) $ \times $ ($ b^n $의 약수)
- $ N $의 약수의 개수 : $ (m+1) \times (n+1) $
$ 18 = 2 \times 3^2 $이므로
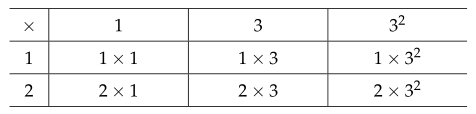
약수는 $ 1 $, $ 2 $, $ 3 $, $ 6 $, $ 9 $, $ 18 $
약수의 개수는 $ (1+1) \times (2+1) = 6 $
2018/07/17 16:17수학 공식