MATH FACTORY

1. 수직선 위의 한 점에 대응하는 수를 그 점의 좌표라 한다.
2. 점 $ {P} $의 좌표가 $ a $라면 $ {P}(a) $로 나타낸다.

1. 두 수직선이 점 $ {O} $에서 서로 수직으로 만날 때, 가로의 수직선을 $ x $축, 세로의 수직선을 $ y $축이라 하고 $ x $축, $ y $축을 통틀어 좌표축이라 한다.
2. 두 좌표축이 만나는 점 $ {O} $를 원점이라 하고, 좌표축이 정해져 있는 평면을 좌표평면이라 한다.

1. 순서를 생각하여 두 수를 짝지어 나타낸 것을 순서쌍이라 한다.
2. 괄호 안에 두 수를 적고, 구분은 쉼표로 한다.
   \begin{gather*}
   (a, \ b)
   \end{gather*}

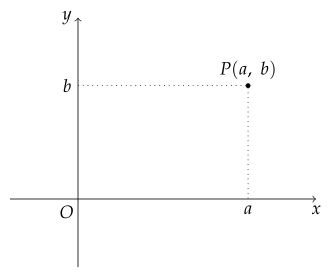
1. 좌표평면 위의 한 점 $ {P} $에서 $ x $축, $ y $축에 각각 수선을 긋고 이 수선이 $ x $축, $ y $축과 만나는 점에 대응하는 수를 각각 $ a $, $ b $라 할 때, 순서쌍 $ (a, \ b) $를 점 $ {P} $의 좌표라 한다. 이때 $ a $를 점 $ {P} $의 $ x $좌표, $ b $를 점 $ {P} $의 $ y $좌표라 한다.
2. 점 $ {P} $의 좌표가 $ (a, \ b) $일 때
   \begin{gather*}
   {P}(a, \ b)
   \end{gather*}와 같이 나타낸다.

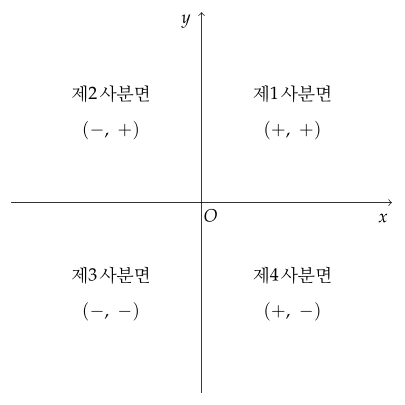
좌표평면은 좌표축에 의하여 $ 4 $개의 부분으로 나누어지는데, 그 각각을 제$ 1 $사분면, 제$ 2 $사분면, 제$ 3 $사분면, 제$ 4 $사분면이라 한다.

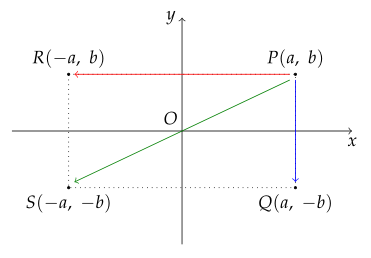
점 $ P(a, \ b) $에 대하여

1. $ x $축에 대하여 대칭인 점 : $ Q(a, \ -b) $
2. $ y $축에 대하여 대칭인 점 : $ R(-a, \ b) $
3. 원점에 대하여 대칭인 점 : $ S(-a, \ -b) $