수학 공식 | 고등학교 > 지수함수와 로그함수의 극한
지수함수의 극한 1
- $ \displaystyle \lim_{x \to r} a^x = a^r $
- $ a>1 $이면 $ \displaystyle \lim_{x \to \infty} a^x = \infty, \ \ \lim_{x \to -\infty} a^x = 0 $
- $ 0 < a < 1 $이면 $ \displaystyle \lim_{x \to \infty} a^x = 0, \ \ \lim_{x \to -\infty} a^x = \infty $
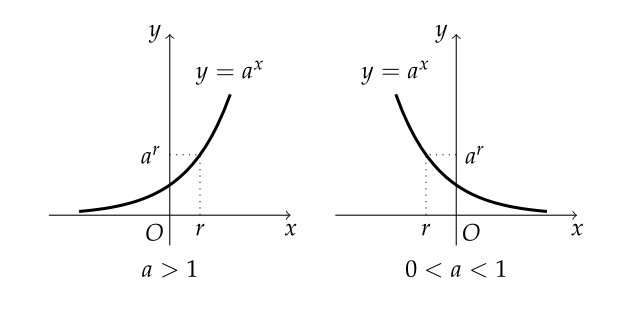
로그함수의 극한 1
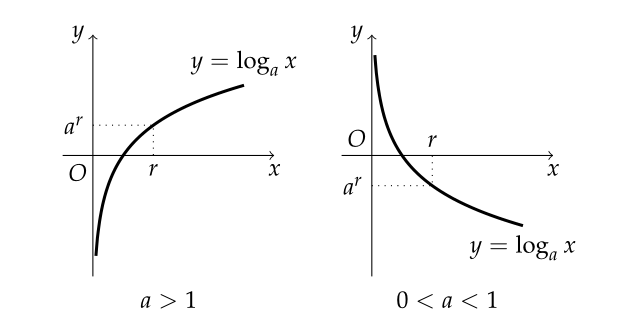
- $ \displaystyle \lim_{x \to r} \log_a x = \log_a r $
- $ a>1 $이면 $ \displaystyle \lim_{x \to \infty} \log_a x = \infty, \ \ \lim_{x \to 0+} \log_a x = -\infty $
- $ 0 < a < 1 $이면 $ \displaystyle \lim_{x \to \infty} \log_a x = -\infty, \ \ \lim_{x \to 0+} \log_a x = \infty $
무리수 $ \boldsymbol{ e } $의 정의
- $ \displaystyle \lim_{x \rightarrow 0} (1+x)^{\frac{1}{x}} = e $
- $ \displaystyle \lim_{x \rightarrow \infty} \left( 1+\frac{1}{x} \right)^{x} = e $
- $ e = 2.718281828459045\cdots $
- $ \displaystyle \lim_{x \rightarrow 0} (1+cx)^{\frac{1}{x}} = \lim_{x \rightarrow 0} (1+cx)^{\frac{1}{cx} \cdot c} = e^c $
- $ \displaystyle \lim_{x \rightarrow \infty} \left( 1+\frac{c}{x} \right)^{x} = \lim_{x \rightarrow \infty} \left( 1+\frac{c}{x} \right)^{\frac{x}{c} \cdot c} = e^c $
자연로그
무리수 $ e $를 밑으로 하는 로그 $ \log_e x $를 $ x $의 자연로그라 하고
\begin{gather*}
\ln x
\end{gather*}
와 같이 나타낸다.
로그함수의 극한 2
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ \ln (1+x) }{x} = 1 $
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ \log_a (1+x) }{x} = \frac{1}{\ln a} $
- $ \displaystyle \lim_{x \to 0} \frac{\ln (1+cx)}{x} = \lim_{x \to 0} \frac{\ln (1+cx)}{cx} \cdot c = c $
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ \log_a (1+cx) }{x} = \lim_{x \rightarrow 0} \frac{ \log_a (1+cx) }{cx} \cdot c = \frac{c}{\ln a} $
- $ \displaystyle \lim_{x \to 0} \frac{\ln (1+x)}{x} = \lim_{x \to 0} \ln (1+x)^{\frac{1}{x}} = \lim_{x \to 0} \ln e = 1 $
- $ \displaystyle \lim_{x \to 0} \frac{\log_a (1+x)}{x} = \lim_{x \to 0} \frac{\ln (1+x)}{x \ln a} = \frac{1}{\ln a} $
지수함수의 극한 2
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ e^x - 1 }{x} = 1 $
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ a^x - 1 }{x} = \ln a $
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ e^{cx} - 1 }{x} = \lim_{x \rightarrow 0} \frac{ e^{cx} - 1 }{cx} \cdot c = c $
- $ \displaystyle \lim_{x \rightarrow 0} \frac{ a^{cx} - 1 }{x} = \lim_{x \rightarrow 0} \frac{ a^{cx} - 1 }{cx} \cdot c = c \ln a $
증명
- $ t = e^x - 1 $로 놓으면 $ x \to 0 $일 때 $ t \to 0 $이고
\begin{gather*}
e^x = 1 + t
\end{gather*}양변에 자연로그를 취하면
\begin{gather*}
x = \ln (1+t)
\end{gather*}이므로
\begin{gather*}
\lim_{x \to 0} \frac{e^x - 1}{x} = \lim_{t \to 0} \frac{t}{\ln (1+t)} = \lim_{t \to 0} \frac{1}{\dfrac{\ln (1+t)}{t}} = 1
\end{gather*} - $ t = a^x - 1 $로 놓으면 $ x \to 0 $일 때 $ t \to 0 $이고
\begin{gather*}
a^x = 1 + t
\end{gather*}양변에 밑을 $ a $로 하는 로그를 취하면
\begin{gather*}
x = \log_a (1+t)
\end{gather*}이므로
\begin{gather*}
\lim_{x \to 0} \frac{a^x - 1}{x} = \lim_{t \to 0} \frac{t}{\log_a (1+t)} = \lim_{t \to 0} \frac{1}{\dfrac{\log_a (1+t)}{t}} = \ln a
\end{gather*}
2018/07/15 20:42수학 공식