수학 공식 | 고등학교 > 표본평균의 분포
모평균, 모분산, 모표준편차
어떤 모집단에서 조사하고자 하는 특성을 나타내는 확률변수를 $ X $라고 할 때, $ X $의 평균, 분산, 표준편차를 각각 모평균, 모분산, 모표준편차라 하고, 각각 기호로 $ m $, $ \sigma^2 $, $ \sigma $와 같이 나타낸다.
표본평균, 표본분산, 표본표준편차
어떤 모집단에서 크기가 $ n $인 표본 $ X_1 $, $ X_2 $, $ \cdots $, $ X_n $을 임의추출하였을 때, 이 표본의 평균, 분산, 표준편차를 각각 표본평균, 표본분산, 표본표준편차라 하고, 각각 기호로 $ \overline{X} $, $ S^2 $, $ S $와 같이 나타내고 다음과 같이 계산한다.
\begin{gather*}
\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i , \ \ S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2
\end{gather*}
표본평균의 평균, 분산, 표준편차
모평균이 $ m $, 모분산이 $ \sigma^2 $인 모집단에서 임의추출한 크기가 $ n $인 표본의 표본평균을 $ \overline{X} $라 할 때, 표본평균 $ \overline{X} $의 평균, 분산, 표준편차는 다음과 같다.
- $ {E(\overline{X})=m} $
- $ \displaystyle {V(\overline{X})}=\frac{\sigma^2}{n} $
- $ \displaystyle {\sigma(\overline{X})}=\frac{\sigma}{\sqrt{n}} $
표본평균의 분포
평균이 $ m $, 분산이 $ \sigma^2 $인 모집단에서 크기 $ n $인 표본을 임의추출할 때
- 모집단이 정규분포 $ N(m, \ \sigma^2) $을 따르면, 표본평균 $ \overline{{X}} $는 정규분포
\begin{gather*}
{N} \left( m, \ \dfrac{\sigma^2}{n} \right)
\end{gather*}을 따른다. - 모집단이 정규분포를 따르지 않아도 $ n $이 충분히 크면 표본평균 $ \overline{{X}} $는 정규분포
\begin{gather*}
{N} \left( m, \ \dfrac{\sigma^2}{n} \right)
\end{gather*}에 가까워진다.
정규분포 $ N(120, \ 10^2) $을 따르는 어떤 모집단에서 크기가 $ 25 $인 표본을 임의추출할 때, 표본평균 $ \overline{X} $에 대하여 확률 $ \mathrm{P}( \overline{X} \leq 125 ) $을 구하여라.
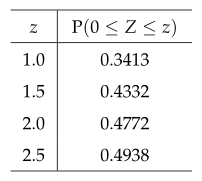
$ \overline{X} $는 정규분포 $ N(120, \ 2^2) $을 따르므로
\begin{gather*}
\mathrm{P} \left( Z \leq \frac{125-120}{2} \right) = \mathrm{P}( Z \leq 2.5 ) = 0.9938
\end{gather*}