수학 공식 | 고등학교 > 삼각함수의 뜻과 그래프
삼각함수
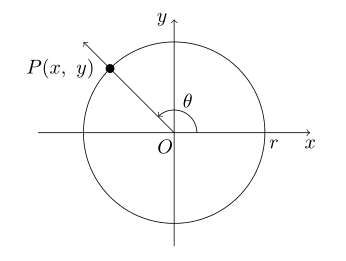
반지름의 길이가 $ r $인 원 위의 점 $ P(x, \ y) $에 대하여 동경 $ OP $가 나타내는 일반각의 크기를 $ \theta $라 할 때
\begin{gather*}
\sin \theta = \frac{y}{r}, \ \ \cos \theta = \frac{x}{r}, \ \ \tan \theta = \frac{y}{x}
\end{gather*}
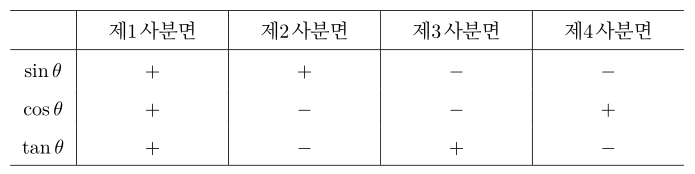
삼각함수의 값의 부호
삼각함수 사이의 관계
- $ \tan \theta = \dfrac{\sin \theta}{\cos \theta} $
- $ \sin^2 \theta + \cos^2 \theta = 1 $
- $ \tan \theta = \dfrac{y}{x} = \dfrac{y/r}{x/r} = \dfrac{\sin \theta}{\cos \theta} $
- $ \sin^2 \theta + \cos^2 \theta = \dfrac{y^2}{r^2} + \dfrac{x^2}{r^2} = \dfrac{x^2 + y^2}{r^2} = \dfrac{r^2}{r^2} = 1 $
삼각함수의 성질
- $ \sin ( 2n\pi + \theta ) = \sin \theta $
$ \cos ( 2n\pi + \theta ) = \cos \theta $
$ \tan ( 2n\pi + \theta ) = \tan \theta $ - $ \sin ( - \theta ) = -\sin \theta $
$ \cos ( - \theta ) = \cos \theta $
$ \tan ( - \theta ) = -\tan \theta $ - $ \sin ( \pi + \theta ) = -\sin \theta $
$ \cos ( \pi + \theta ) = -\cos \theta $
$ \tan ( \pi + \theta ) = \tan \theta $ - $ \sin ( \pi - \theta ) = \sin \theta $
$ \cos ( \pi - \theta ) = -\cos \theta $
$ \tan ( \pi - \theta ) = -\tan \theta $ - $ \sin \left( \dfrac{\pi}{2} + \theta \right) = \cos \theta $
$ \cos \left( \dfrac{\pi}{2} + \theta \right) = -\sin \theta $
$ \tan \left( \dfrac{\pi}{2} + \theta \right) = - \dfrac{1}{\tan \theta} $ - $ \sin \left( \dfrac{\pi}{2} - \theta \right) = \cos \theta $
$ \cos \left( \dfrac{\pi}{2} - \theta \right) = \sin \theta $
$ \tan \left( \dfrac{\pi}{2} - \theta \right) = \dfrac{1}{\tan \theta} $
삼각함수의 각 변형 방법
- 각 변형하기
주어진 각을 $ 90^\circ \times n \pm \alpha^\circ $ 또는 $ \dfrac{\pi}{2} \times n \pm \theta $의 꼴로 변형한다. (단, $ n $은 정수) - 삼각함수 정하기
$ n $이 짝수이면 그대로, $ n $이 홀수이면 $ \sin $은 $ \cos $으로, $ \cos $은 $ \sin $으로, $ \tan $는 $ \dfrac{1}{\tan} $로 바꾼다. - 부호 정하기
$ \alpha^\circ $, $ \theta $를 예각으로 간주하고, 처음 주어진 삼각함수의 부호를 따른다.
다음 식을 간단히 하여라.
\begin{gather*}
\sin (\pi + \theta) + \cos (\pi - \theta) + \sin \left( \frac{\pi}{2} + \theta \right) + \cos \left( \frac{\pi}{2} - \theta \right)
\end{gather*}
$ -\sin\theta - \cos\theta + \cos\theta + \sin\theta = 0 $
주기와 주기함수
상수함수가 아닌 함수 $ f(x) $의 정의역에 속하는 모든 $ x $에 대하여
\begin{gather*}
f(x+p) = f(x)
\end{gather*}
를 만족하는 $ 0 $이 아닌 상수 $ p $가 존재할 때, 함수 $ f(x) $를 주기함수라 하고, 상수 $ a $의 값 중 최소의 양수를 주기라고 한다.
삼각함수의 그래프
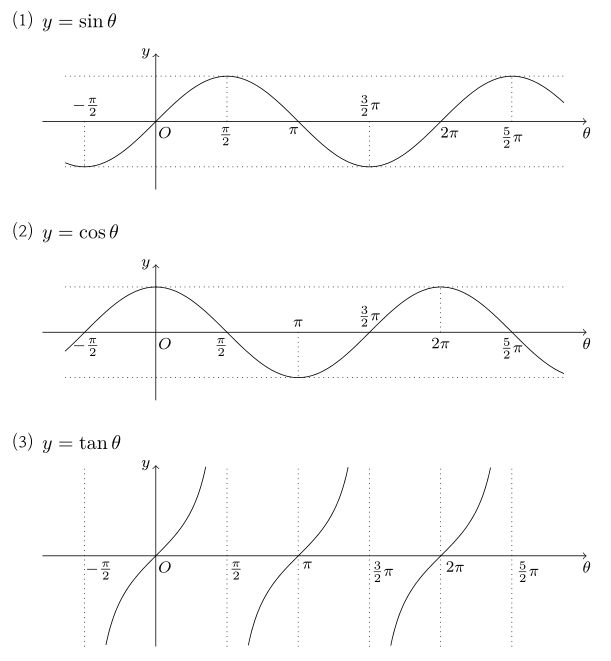
삼각함수의 그래프의 성질

함수 $ f(x) = a \sin bx + c $의 최댓값은 $ 5 $, 최솟값은 $ -3 $, 주기는 $ 4\pi $이다. $ f(\pi) $의 값을 구하여라. (단, $ a>0 $, $ b>0 $)
최댓값이 $ 5 $이므로 $ a + c = 5 $
최솟값이 $ -3 $이므로 $ -a+c=-3 $
주기가 $ 4\pi $이므로 $ \dfrac{2\pi}{b} = 4\pi $
$ \therefore \ \ \ a=4, \ \ b = \dfrac{1}{2}, \ \ c=1$
$ f(x) = 4 \sin \dfrac{1}{2} x + 1 $이므로
$ f(\pi) = 4 \sin \dfrac{\pi}{2} + 1 = 5 $
삼각방정식
삼각함수의 각의 크기를 미지수로 하는 방정식을 삼각방정식이라 한다.
삼각방정식의 풀이
- 주어진 방정식을 $ \sin x = k $ ($ \cos x = k $, $ \tan x = k $)의 꼴로 바꾼다.
- 주어진 범위에서 $ y = \sin x $ ($ y=\cos x $, $ y=\tan x $)의 그래프와 직선 $ y=k $를 그린다.
- 삼각함수의 그래프와 직선의 교점의 $ x $좌표가 방정식의 해이다.
$ 0 \leq x \leq 2\pi $일 때, 다음 방정식의 해를 구하여라.
\begin{gather*}
\sin x = \frac{1}{2}
\end{gather*}
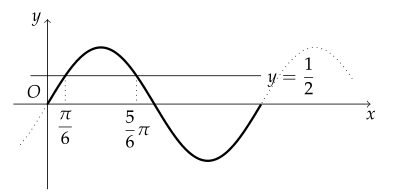
방정식의 해는 $ x = \dfrac{\pi}{6} $ 또는 $ x = \dfrac{5}{6}\pi $이다.
삼각부등식
삼각함수의 각의 크기를 미지수로 하는 부등식을 삼각부등식이라 한다.
삼각부등식의 풀이
- 주어진 부등식을 $ \sin x > k $ ($ \cos x > k $, $ \tan x > k $) 등의 꼴로 바꾼다.
- 주어진 범위에서 $ y = \sin x $ ($ y=\cos x $, $ y=\tan x $)의 그래프와 직선 $ y=k $를 그린다.
- 그래프를 이용하여 부등식의 해를 구한다.
$ 0 \leq x \leq 2\pi $일 때, 다음 방정식의 해를 구하여라.
\begin{gather*}
\cos x < \frac{1}{2}
\end{gather*}
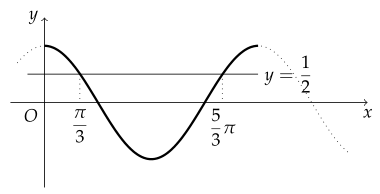
부등식의 해는 $ \dfrac{\pi}{3} < x < \dfrac{5}{3}\pi $이다.