수학 공식 | 고등학교 > 미지수가 1개인 연립일차부등식
연립부등식
- 두 개 이상의 부등식을 한 쌍으로 묶어 나타낸 것을 \jbTextBf{연립부등식}이라 한다.
- 각 부등식을 동시에 만족하는 미지수의 값 또는 범위를 \jbTextBf{연립부등식의 해}라 한다.
- 연립부등식의 해를 구하는 것을 \jbTextBf{연립부등식을 푼다}고 한다.
미지수가 1개인 연립일차부등식의 풀이
각 부등식의 해를 수직선 위에 나타내고, 공통부분을 찾아 부등호를 사용하여 나타낸다.
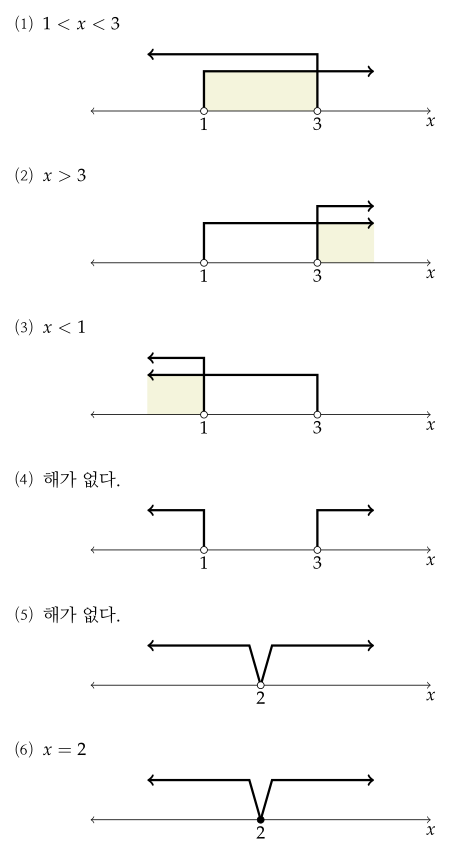
다음 부등식을 풀어라.
⑴ $ \begin{cases} \ x > 1 \\ \ x < 3 \end{cases} $
⑵ $ \begin{cases} \ x > 1 \\ \ x > 3 \end{cases} $
⑶ $ \begin{cases} \ x < 1 \\ \ x < 3 \end{cases} $
⑷ $ \begin{cases} \ x < 1 \\ \ x > 3 \end{cases} $
⑸ $ \begin{cases} \ x < 2 \\ \ x > 2 \end{cases} $
⑹ $ \begin{cases} \ x \leq 2 \\ \ x \geq 2 \end{cases} $
$ \boldsymbol{ A<B<C } $ 꼴의 부등식
$ \begin{cases} \ A<B \\ \ B<C \end{cases} $ 꼴로 바꾸어서 푼다.
2018/06/19 12:36수학 공식