수학 공식 | 고등학교 > 구분구적법
구분구적법
도형의 넓이나 부피를 구할 때, 주어진 도형을 작은 기본 도형으로 잘게 나누어 값을 구하고 그 값의 합의 극한값으로 도형의 넓이나 부피를 구하는 방법을 구분구적법이라 한다.
밑변의 길이가 $ a $이고 높이가 $ h $인 이등변삼각형의 넓이를 구분구적법으로 구하여라.
이등변삼각형의 높이를 $ n $등분하고, 각 분점을 지나면서 밑면에 평행한 선분을 밑변으로 하는 $ n $개의 직사각형을 만든다.
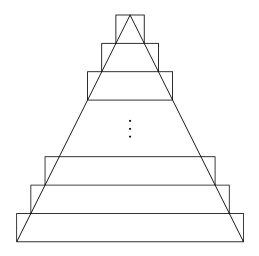
직사각형의 넓이의 합을 $ S_n $이라 하면
\begin{align*}
S_n &= \frac{a}{n} \cdot \frac{h}{n} + \frac{2a}{n} \cdot \frac{h}{n} + \cdots + \frac{na}{n} \cdot \frac{h}{n} \\
&= \sum_{k=1}^{n} \frac{ka}{n} \cdot \frac{h}{n} = \frac{ahn(n+1)}{2n^2}
\end{align*}
따라서 이등변삼각형의 넓이는
\begin{align*}
\lim_{n \to \infty} S_n = \lim_{n \to \infty} \frac{ahn(n+1)}{2n^2} = \frac{1}{2} ah
\end{align*}
2018/06/05 15:37수학 공식