수학 공식 | 고등학교 > 거듭제곱근의 뜻과 성질
거듭제곱
- 실수 $ a $와 양의 정수 $ n $에 대하여 $ a $를 $ n $번 거듭하여 곱한 것을 $ a $의 $ n $제곱이라 하고, $ a^n $으로 나타낸다.
- 이때 $ a $, $ a^2 $, $ a^3 $, $ \cdots $, $ a^n $, $ \cdots $을 통틀어 $ a $의 거듭제곱이라 하고, $ a $를 거듭제곱의 밑, $ n $을 거듭제곱의 지수라 한다.
거듭제곱근
- 실수 $ a $와 $ 2 $ 이상의 자연수 $ n $에 대하여 $ n $제곱하여 $ a $가 되는 수, 즉 $ x^n=a $를 만족시키는 $ x $를 $ a $의 $ n $제곱근이라 한다.
- 이때 $ a $의 제곱근, $ a $의 세제곱근, $ a $의 네제곱근, $ \cdots $을 통틀어 $ a $의 거듭제곱근이라 한다.
- 복소수 범위에서 실수 $ a $의 $ n $제곱근은 $ n $개가 있다.
실수인 거듭제곱근
- $ n $이 홀수이면, 실수 $ a $의 $ n $제곱근 중 실수인 것은 한 개 있고, 이것을 $ \sqrt[n]{a} $로 나타낸다.
- $ n $이 짝수이면,
$ a > 0 $일 때, $ a $의 $ n $제곱근 중 실수인 것은 두 개 있고, 그 중 양수를 $ \sqrt[n]{a} $, 음수를 $ -\sqrt[n]{a} $로 나타낸다.
$ a=0 $일 때, $ a $의 $ n $제곱근은 $ 0 $이다.
$ a<0 $일 때, $ a $의 $ n $제곱근 중 실수인 것은 없다.

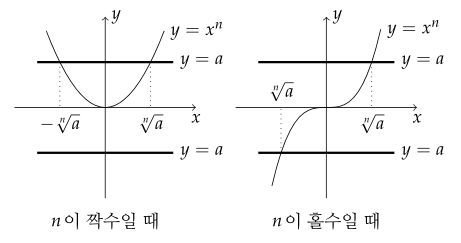
좌표평면에서 $ y=x^n $의 그래프와 직선 $ y=a $의 교점의 $ x $좌표가 $ a $의 $ n $제곱근 중 실수이다.
다음 명제의 참, 거짓을 판별하시오.
- $ 64 $의 세제곱근은 $ \sqrt[3]{64} $뿐이다.
- $ -13 $의 세제곱근 중 실수인 것은 없다.
- $ 16 $의 네제곱근 중 실수인 것은 $ \sqrt[4]{16} $뿐이다.
- $ \sqrt[4]{-16} $은 $ -16 $의 네제곱근 중 하나이다.
- $ n $이 짝수일 때 $ -7 $의 $ n $제곱근 중 실수인 것은 두 개이다.
- 거짓. 허수까지 포함하여 $ 3 $개 있다.
- 거짓. 하나 있다.
- 거짓. $ -\sqrt[4]{16} $도 있다.
- 거짓. 근호는 실수일 때 사용한다.
- 거짓. 없다.
거듭제곱근의 성질
$ a>0 $, $ b>0 $이고, $ m $, $ n $이 $ 2 $ 이상의 정수일 때
- $ (\sqrt[n]{a})^n = a $
- $ \sqrt[n]{a} \sqrt[n]{b} = \sqrt[n]{ab} $
- $ \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}} $
- $ \left( \sqrt[n]{a} \right)^m = \sqrt[n]{a^m} $
- $ \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} = \sqrt[n]{\sqrt[m]{a}} $
- $ \sqrt[np]{a^{mp}} = \sqrt[n]{a^m} $ (단, $ p $는 양의 정수)
다음 식을 간단히 하여라.
- $ \sqrt[3]{4} \times \sqrt[3]{16} $
- $ \dfrac{\sqrt[4]{64}}{\sqrt[4]{4}} $
- $ ( \sqrt[4]{9} )^2 $
- $ \sqrt[12]{3^4} \times \sqrt[9]{3^6} $
- $ \sqrt{\sqrt[3]{16}} \times \sqrt[4]{\sqrt[3]{16}} $
- $ \sqrt[3]{4 \times 16} = \sqrt[3]{4^3} = 4 $
- $ \sqrt[4]{16} = \sqrt[4]{2^4} = 2 $
- $ \sqrt[4]{9^2} = \sqrt[4]{3^4} = 3 $
- $ \sqrt[3]{3} \times \sqrt[3]{3^2} = \sqrt[3]{3^3} = 3 $
- $ \sqrt[6]{16} \times \sqrt[12]{16} = \sqrt[12]{16^2} \times \sqrt[12]{16} = \sqrt[12]{2^{12}} = 2 $
2017/11/25 01:33수학 공식