두 점을 지름의 양 끝으로 하는 원의 방정식
원의 방정식을 만들기 위해서는 원의 중심의 좌표와 반지름의 길이가 필요합니다. 만약 지름의 양 끝에 있는 두 점의 좌표가 주어진다면, 두 점의 중점이 원의 중심이 되고, 두 점 사이의 거리의 반이 반지름의 길이가 되므로, 원의 방정식을 구할 수 있습니다.
원주각의 성질과 피타고라스의 정리를 이용하는 또 다른 방법이 있는데, 그걸 한 번 알아보겠습니다.
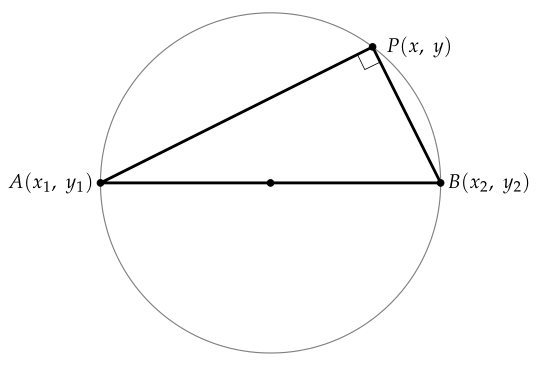
좌표평면 위의 두 점 $ A(x_1, \ y_1) $과 $ B(x_2, \ y_2) $를 지름의 양 끝으로 하는 원이 있다고 하겠습니다.
원 위의 점을 $ P(x, \ y) $라 하면, 반원에 대한 원주각의 크기는 $ 90^\circ $이므로, 피타고라스의 정리에 의하여
\begin{gather*}
\overline{AP}^2 + \overline{BP}^2 = \overline{AB}^2
\end{gather*}
이 성립합니다. 즉
\begin{gather*}
(x-x_1)^2 + (y-y_1)^2 + (x-x_2)^2 + (y-y_2)^2 \\
= (x_2-x_1)^2 + (y_2-y_1)^2
\end{gather*}
이고, 이를 정리하면
\begin{gather*}
(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = 0
\end{gather*}
이 됩니다.
공식을 기억할 수 있다면 쉽게 답을 구할 수 있습니다. 공식을 몰라도 답은 쉽게 구할 수 있는데, 시간이 좀 더 걸리겠죠.
좌표평면 위의 두 점 $ A(1, \ 2) $과 $ B(9, \ 8) $을 지름의 양 끝으로 하는 원의 방정식을 구하여라.
방법 1
$ (x-1)(x-9) + (y-2)(y-8) = 0 $
$ \therefore \ \ (x-5)^2 + (y-5)^2 = 5^2 $
방법 2
두 점 $ A $와 $ B $의 중점의 좌표 $ (5, \ 5) $, 선분 $ AB $의 길이는 $ 10 $이다.
즉, 중심의 좌표가 $ (5, \ 5) $, 반지름의 길이가 $ 5 $인 원이므로
$ (x-5)^2 + (y-5)^2 = 5^2 $